 ANTENNAS FROM THE GROUND UP
ANTENNAS FROM THE GROUND UP
In our last episode, we explored the nature and losses of some common ATU networks, namely, the C-L-C PI, the C-L-C Tee, and the SPC. This time, we shall look at L-C-L Tees, McCoyþs Ultimate Transmatch, and simple 2-element L-C networks. The tables showing the trends in ë continue to be for 10.1 MHz. Values of capacitance and inductance will vary for the frequency in use, but the values of delta will remain the same for the same input and output values of resistance and reactance at any HF frequency.
We are restricting ourselves here to networks, and we have set aside inductively coupled matching circuits. In some future installment, we shall examine these circuits, which are capable of excellent efficiency but suffer in many cases from some mechanical inconveniences for multiband use. Among commonly used wide-band inductively coupled ATUs on todayþs market, perhaps only the Z- match overcomes, at least for QRP operation, most of the mechanical problems. But let's, for the moment. return to our network programming.
L-C-L Tees: The L-C-L Tee, shown in Figure 1, has suffered from neglect until recent years. It is a natural low- pass filter, like the C-L-C PI shown earlier. However, whereas the intermediate impedance of the PI is lower than either the input or output impedances, the intermediate impedance of the L-C-L Tee is higher than either the input or output impedances. This results in higher voltages and lower currents at the junction of the three components.
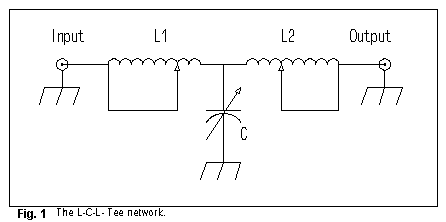
Determining delta for the L-C-L Tee requires attention to both inductors, which for simplicity are assumed to have the same Q in the following Egan equation:
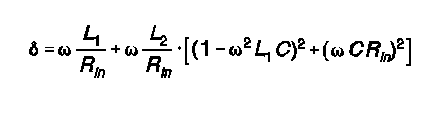
Input = 50 Ohms; Output = 150 +/- j0 Ohms
Minimum permitted L1 = 1.114 µH
L1 1.115 L2 0.07 C 152 Delta 1.4
L1 1.12 L2 0.20 C 157 Delta 1.5
L1 1.20 L2 0.77 C 176 Delta 1.8
Input = 50 Ohms; Output = 150 + j100 Ohms
Minimum permitted L1 = 1.438 µH
L1 1.439 L2 0.01 C 181 Delta 1.8
L1 1.50 L2 0.16 C 180 Delta 2.0
L1 2.00 L2 1.30 C 159 Delta 3.1
Input = 50 Ohms; Output = 150 - j100 Ohms
Minimum permitted L1 = 1.114 µH
L1 1.115 L2 1.51 C 145 Delta 2.1
L1 1.12 L2 1.38 C 140 Delta 2.0
L1 1.14 L2 1.16 C 129 Delta 1.9
L1 1.43 L2 0.02 C 85 Delta 1.8
Despite the use of two theoretically lossy inductances in the L-C-L Tee, it maintains low values of ë over a wide range of load conditions and transformation settings. Delta climbs more rapidly with inductive loads than with capacitive loads away from optimal settings. The operative rule of thumb for maximum efficiency is this:
L-C-L Tees: Choose the lowest value of L2 that permits a match.
This operative rule holds true at higher ratios of output-to-input impedance, even though values of delta increase at those ratios. L-C-L Tees are subject to losses from circulating currents in the shorted turns of either switched or rotary solenoid or toroid coils, losses that the value of ë cannot take into account. Therefore, construction of this network requires special care.
Ultimate Transmatch: Lew McCoy's Ultimate Transmatch (UT) is an interesting variation on the C-L-C Tee. It places a dual capacitor at the input of the network, one section in series with the signal path, the other section to ground. Figure 2 shows the general outline of the network.
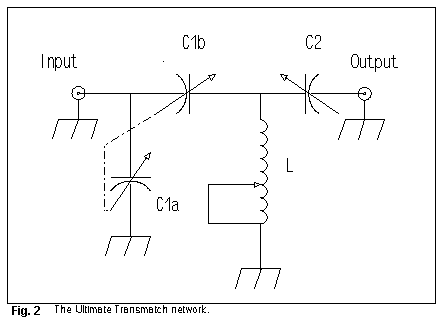
Calculating delta for the UT design requires the following Egan equation:
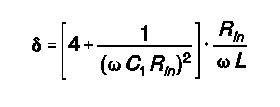
Input = 50 Ohms; Output = 150 +/- j0 Ohms Maximum permitted C1 = 750 pF per section C1 749 C2 168 L 0.57 Delta 5.8 C1 600 C2 161 L 0.68 Delta 5.0 C1 400 C2 143 L 0.90 Delta 4.1 C1 250 C2 113 L 1.17 Delta 3.8 Input = 50 Ohms; Output = 150 + j100 Ohms Maximum permitted C1 = 750 pF per section C1 749 C2 81 L 0.57 Delta 5.8 C1 400 C2 75 L 0.90 Delta 4.1 C1 250 C2 66 L 1.17 Delta 3.8 Input = 50 Ohms; Output = 150 - j100 Ohms Maximum permitted C1 = 546 pF per section C1 545 C2 >350K L 0.73 Delta 4.7 C1 300 C2 615 L 1.06 Delta 3.8 C1 250 C2 400 L 1.17 Delta 3.8 C1 200 C2 256 L 1.30 Delta 3.9
Like other series-capacitance designs, the UT appears most effective with purely resistive and inductive loads: Required values for a match fall easily within the ranges of normal components just as the network approaches maximum efficiency. (If C1 is lowered further in these cases, delta increases.) However, with capacitively reactive loads, maximum efficiency has passed by the time C2 enters the range most normal for ATUs.
Although the values for delta are higher than with some other designs, efficiency remains in the 96% ballpark. In fact, the efficiency of the Ultimate Transmatch appears to increase (at least to some limit) with increases in the ratio of output-to-input impedance. Using a 300-Ohm output resistance with either no reactance or 100 Ohms of inductive reactance, the UT achieved values of delta in the neighborhood of 2.8, while with 100 Ohms of capacitive reactance, delta was about 3.5. The rule of thumb for the UT design is not as simple as with some other designs:
UT: With normal ATU components (Cmax less than 400 pF), choose the highest value of C2 that permits a match within the range of C1.
Remember that, for any of the network designs, as the frequency decreases, some of the efficiencies achieved in these 10.1 MHz tables may not be reached, since proportionately greater values of C and L may be needed for the same load conditions. Moreover, switched inductors may not provide the values necessary for highest efficiencies. This limitation is rarely a problem, since the value of delta in most cases "bottoms out" over a fairly wide range. Nonetheless, the rules of thumb continue to apply.
Moreover, remember that these figures are based solely on losses in the inductor, one assumed to have a Q in the range of 100. Additional losses due to poor components, bad wiring and switching, stray inductances and capacitances, and coil "suck-out" are not accounted for by the calculations. If components get warm or arc under matched conditions at 100 watts, even though the calculations indicate less than 5% losses, believe your senses. Then analyze the components and construction of your ATU. Something other than network choice is very wrong.
2-Element L-Circuits: Although less versatile than 3-element networks, 2- element networks (L-circuits) are more fundamental. Each circuit consists of a series reactance and a parallel (shunt) reactance. The shunt reactance goes at either the input or the output side of the circuit depending upon whether one is transforming an impedance downward or upward, respectively. The reactances are normally of opposite types.
Thought of in terms of reactance, rather than components, the reactances can be swapped with respect to type for the same impedance transformation. This will, of course, change the component values.
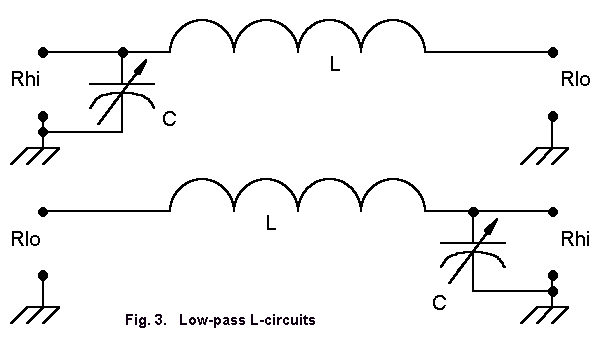
Figure 3 shows two L-circuits, one for transformation upward, the other for transformation downward. As given, L is the series reactance and C is the shunt reactance. The result is a low pass filter. Had we placed L in the shunt position and C in the series position, we would have a high pass filter.

Figure 4 redraws the L-circuits in their high-pass configurations. The top circuit, transforming downward, is the basis for the Beta-match, where the capacitance is actually a function of shortening the antenna element rather than being a separate lumped component.
It is possible to treat the input and output impedances as purely resistive, as done in Figure 3, and then to add on any capacitive or inductive reactance necessary to cancel out load reactances. If we follow this procedure, the delta figure for the L-circuit simplifies to the follow expression:
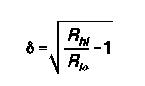
Then, the required series and shunt reactances (Xs and Xp) can be calulated from simple equations:
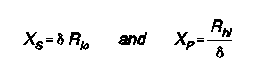
Convert these figures to a capacitance and an inductance by use of the usual equations involving 2piF.
When the load presented to an L-circuit is complex, that is, when it contains both resistance and reactance, the calculation of delta becomes somewhat more complex. However, we can show the trends by looking at our test case at 10.1 MHz. With L-circuits, with some exceptions in small regions where designs overlap under certain reactive loads, only one set of values provides a desired impedance transformation.
In each test case, we shall be transforming an impedance of 50 Ohms upward, so the Rlo-to-Rhi versions of the L-circuits will apply. The interesting data will concern what happens to delta as we add either inductive or capacitive reactance. (LP = low-pass configuration; HP = high-pass configuration.)
Input = 50 Ohms; Output = 150 Ohms LP: Ls 1.114 µH Cp 148.6 pF Delta 1.41 HP: Cs 222.9 pF Lp 1.671 µH Delta 1.41 Input = 50 Ohms; Output = 150 + 100 Ohms LP: Ls 1.438 µH Cp 181.3 pF Delta 1.83 HP: Cs 172.6 pF Lp 2.946 µH Delta 1.16 Input = 50 Ohms; Output = 150 - 100 Ohms LP: Ls 1.438 µH Cp 84.3 pF Delta 1.83 HP: Cs 172.6 pf Lp 1.370 µH Delta 2.49
Note that when the load is purely resistive, the high-pass and the low- pass configurations are equally efficient, that is, they have the same value of delta. When the load is inductively reactive, the high-pass configuration has the lower value of delta and thus has lower losses. When the load is capacitively reactive, the low- pass configuration has the advantage.
Traditionally, we have built L-circuit tuners in the low-pass configuration for mechanical ease, not for the added filtering of transmitted signals. The attenuation of harmonics in a single L- circuit is somewhat minimal at best. However, most variable capacitors with any power-handling capability have ground rotator plates, and traditional construction has called for a metal chassis or case.
Now add to this situation the fact that few hams have bothered to calculate the network efficiency of even the simple L-circuit (let alone other networks). Hence, they knew only that they either did or did not have a match. At power levels from 50 watts upward, the additional tuner losses seem to make little difference to the average operator. As a consequence, the high- pass L-circuit configuration has been neglected in all but Beta matches to Yagis and other low-impedance antennas.
At QRP, where every avoidable loss is to be eliminated, the high-pass configuration for inductively reactive loads should be considered, especially in cases where the inductive reactance is high. Switches and jumpers can adapt the same coil and capacitor to use in high-pass, low-pass, high-to-low impedance, and low-to-high impedance combinations. Since the ATU network, whatever its configuration, is composed of passive components, no shielding is necessary. Non-metallic cases are not only satisfactory, they in fact reduce many stray capacitances that lower the overall component Q within the network.
Single-Ended Networks: All of the networks we have examined for efficiency (or losses, to look at the other side of the coin) are single-ended or unbalanced. Many of the uses to which they are put involve parallel or balanced transmission line. From early days, we have been taught not to use a single-ended network on balanced lines. ATU manufacturers who use unbalanced networks often install a 4:1 balun or transmission-line transformer between the network and a pair of so- called balanced output terminals.
As we saw in a past installment, high impedance loads with large reactive components on balanced transmission lines do not present high impedances to the ATU terminals for most of each half-wavelength of transmission line. Just the opposite prevails: the load the ATU sees is a very low impedance that needs no division by 4. Moreover, transmission-line transformers are efficient only with nearly pure resistive loads, and the best expert recommendations consistently tell us to compensate for reactance at the antenna terminals. We can effect a match that achieves a low SWR for the transmitter-to-line junction, but at indeterminate loss levels.
So what can we do? Two answers have emerged from amateur experience.
1. Some amateurs have found that, at least for their situations, the seemingly unbalanced network introduces no serious imbalance in currents and voltages along the transmission line. By floating the case, that is, leaving it ungrounded, the network performs normally and yields a perfectly or nearly perfectly balanced output. If a 1:1 balun or a line isolator (a W2DU- type balun choke or a series of split ferrite cores) is placed on the transmitter side of the ATU, any currents that remain on the outside of the coax are effectively blocked from the transmitter and other equipment cases.
2. Other amateurs have had good success by transitioning to unbalanced line either at the ATU-to-transmission line junction or within a few feet of the ATU--perhaps at a window sill. Again, a line isolator prevents RF currents from flowing on the outside of the ATU case or the short section of coaxial line from the ATU to the window sill. The series section of coxial line introduces an altered impedance transformation and does impart some loss. Even the line isolator is not completely lossless, as W2FMI found some heating of the core material nearest the load in testing the W2DU balun under high power. However, the losses may be less than those accompanying alternative techniques of feeding power to the antenna. In such cases, this method may prove attractive.
In the end, decisions fall into the domain of the practical. What is the most efficient and least lossy method of feeding my antenna among the practical alternatives I have? However, the more we know about networks, the greater the number of our alternatives.
Updated 3-11-99. © L. B. Cebik, W4RNL. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.