 ANTENNAS FROM THE GROUND UP
ANTENNAS FROM THE GROUND UP
Losses from the insertion of antenna tuning units or transmatches between transmitters and transmission lines have bothered numerous folks for some time. There are two questions: how much loss can I expect? and how do I minimize the loss? Both are good questions with good answers. Unfortunately, they are not super simple answers. But some old material combined with some new material can make the answers easier to come by. Those who like the math involved can focus on the equations, while those interested in operational matters can concentrate on the tables and the resulting rules of thumb to minimize losses.
Most of this installment and the next appeared originally in QRP Quarterly for January, 1996. I have added some material, especially about 2-element L-C ATUs, and rearranged some of the ideas. This review of the estimate of losses in ATUs is also a good review of the most common types of network ATUs in use in amateur circles these days.
Most ATUs used today are L-C networks. The most common configuration is the C-L-C Tee network. However, L-C-L Tees and C-L-C PIs are in use, as are SPC and Ultimate Transmatch designs. Loss figures can be calculated for all such networks.
The old material that contributes to determining ATU losses appears in Terman's Radio Engineers' Handbook (McGraw-Hill, 1943), pages 210-215. Based predominantly on work done in the 1930s by W.I. Everitt, Terman's analysis of classic impedance-matching networks is still referenced by current handbooks. The relevant part for considering ATU losses is the term, delta, which is a justifiably simplified measure of power dissipation in networks. For any impedance matching network, the primary power dissipation culprit is the inductance, and inductor losses can be calculated.
The efficiency of L-C networks is dependent upon the impedance transformation ratio and the phase shift. PI networks and L-C-L Tees generally exhibit a large angle of phase retardation, while the C-L-C Tee circuit shows a large angle of phase advance. In contrast, simple L-networks show small angles of phase advance or retardation. Losses increase with increasing transformation ratios and tend to be larger when the phase shift is either very large or very small. The delta figure takes both into account. (Note, in some explanations of networks, but not in all, Terman's delta goes under the name of "working Q," "circuit Q," or "network Q.")
The concept of delta has certain limitations. First, it ignores capacitor losses. This is justified for well- designed capacitors at HF and below, but capacitor losses may become significant at the boundary between HF and VHF (about 30 MHz). Second, the loss figure ignores the effects of strays, both capacitive and inductive, within a real ATU, especially one cramped inside a metal case. At 10 meters, the principal L and C in a matching circuit may be composed more of strays than of component values. Third, the technique will assume we know the coil Q in figuring ultimate efficiency and losses. On this score, we mostly guess, but a figure of 100 for good air wound coils is a conservative guess. Good powdered iron core toroids may yield more. Of course, the "suck out" effect of shorted coil turns is also ignored. Moreover, only networks, and not inductively coupled ATUs, are covered.
The developer of the mathematical analysis used here, ZL1LE, recently ran a comparison between delta calculations and a more complex analysis published in QEX. The results showed an exceptionally high degree of correlation above load impedances in the 20-25 Ohms range, with the delta calculations being the more pessimistic below that level.
Within these limits, the Terman-Everitt delta yields a fair estimate of loss and efficiency. As Terman notes,

In other, equally approximate terms, network efficiency = 1 - delta/Q. (Multiply this figure times 100 for a percentage value of efficiency).
Now if we only knew how to calculate delta, the rest would be simple. Terman provides graphs for estimating delta. Each type of network requires its own calculation, and it can be a bit tedious to calculate delta for several combinations of component settings. However, Brian Egan, ZL1LE, has derived equations for delta-calculations and added them to his program TUNER.BAS. This versatile program is now included in the collection of programs called HAMCALC, made available by George Murphy. See preceding installments for how to obtain a copy of HAMCALC and Murph's frequent upgrades.
Among the networks for which ZL1LE includes calculations are PIs, C-L-C Tees, SPCs, Ultimates, and L-C-L Tees. By running the program through a selection of values, one can learn the trends of tuning that will minimize losses. Operationally, that is the best we can hope for with a fixed set of impedance conditions presented by the transmission line from the antenna. From the general relationship of power lost to power delivered, it is clear that we always want to tune for minimum delta.
For almost any loed presented to the tuner, there is usually more than one set of values for the ATU components that will effect a match so that the SWR meter shows a 1:1 SWR ratio. Not every combination is of equal quality in terms of losses within the ATU. Any limitations we encounter on the range of component variability-- such as switched coil taps or switched fixed capacitors--can also limit our ability to achieve the lowest possible loss setting.
I ran TUNER.BAS through a number of exercises, and here are some results for some configurations. I chose 10.1 MHz, because I was working on a network problem for that band. To standardize the tests, I chose the following load conditions for each network: 150 +/- j0 Ohms, 150 + 100 Ohms, and 150 - j100 Ohms. Looking at a straight 3:1 SWR purely resistive load is a good beginning point, while exploring the network with both capacitive and inductive reactances indicates limitations of the network with certain types of loads. This test is limited, since a higher delta at a 3:1 impedance transformation ratio is not indicative of the network's overall capability. Some networks are more efficient with lower transformation ratios, while others grow more efficient as the transformation ratio increases.
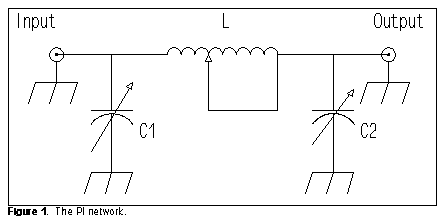
PIs: This familiar low-pass network configuration appears in Figure 1.
For those interested, the Egan equation for delta for a PI network (where omega = 2piF wherever it occurs) is the following:
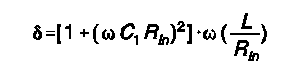
Here is a small table of results for 10.1 MHz:
Input = 50 Ohms; Output = 150 =/- j0 Ohms;
Maximum permitted L = 1.365 µH
L 1.364 C1 172 C2 179 delta 2.2
or 1.364 192 185 2.5
L 1.2 C1 36 C2 150 delta 1.5
L 1.15 C1 15 C2 149 delta 1.5
Input = 50 Ohms; Output = 150 + j100 Ohms
Maximum permitted L = 1.640 µH
L 1.639 C1 140 C2 197 delta 2.5
L 1.6 C1 84 C2 187 delta 2.2
L 1.5 C1 26 C2 182 delta 1.9
Input = 50 Ohms; Output = 150 - j100 Ohms
Maximum permitted L = 1.640 µH
L 1.639 C1 140 C2 100 delta 2.5
L 1.6 C1 84 C2 90 delta 2.2
L 1.5 C1 26 C2 85 delta 1.9
In all three cases, the lists stop where one of the values approaches the minimum usually obtainable with ordinary components. In this case, a value for C1 lower than about 20 pF is not normal for most ATUs. In many instances, as illustrated by the very first entry, two solutions to the matching problem are possible. After the first entry, only the more promising set of values is shown. PI networks are, within limits, equally capable of handling capacitive and inductive reactances in the load, with the limits of both being related to the range of C2. Notice that efficiencies of 98% are possible within the limits of the method. As Terman notes, increasing the ratio of the impedances to be matched increases the value of delta and decreases efficiency. For example, when the resistive component of the output impedance is 300 Ohms, with or without a reactive load, the lowest value of delta is about 2.3. To achieve the highest efficiency possible for any given matching situation, we must use the following rule of thumb:
PI networks: Use the lowest value of L that still permits C1 to be effective.
C-L-C Tees: This most common ATU network configuration appears in Figure 2.

Whereas the PI network is a natural low-pass filter, the C-L-C network is a natural high-pass filter. However, this fact does not hamper its ability to match a wide range of complex load impedances.
To determine delta, use the Egan equation

Input = 50 Ohms; Output = 150 +/- j0 Ohms
Maximum permitted C1 = 222.9 pF
C1 222.8 C2 6027 L 1.65 delta 1.4
C1 222 C2 1468 L 1.59 delta 1.5
C1 220 C2 992 L 1.56 delta 1.5
C1 210 C2 362 L 1.43 delta 1.8
C1 200 C2 262 L 1.39 delta 2.0
Although a very low value of delta is theoretically possible, a realistic value of 2.0 or higher is to be expected with common components used in ATUs. As with a PI network, the C-L-C Tee yields higher values of delta as the output impedance is increased. At 6:1 ratio of output-to-input impedance, delta does not go below 2.1 with normal ATU components.
Input = 50 Ohms; Output = 150 + j100 Ohms
Maximum permitted C1 = 222.9 pF
C1 222.8 C2 154 L 1.65 delta 1.4
C1 220 C2 132 L 1.54 delta 1.6
or 220 196 1.85 1.3
C1 210 C2 110 L 1.43 delta 1.8
or 210 279 2.12 1.2
C1 200 C2 98 L 1.39 delta 2.0
or 200 396 2.34 1.2
In this table, two sets of matching values are possible, even within the range of normal ATU components. One set drives toward maximal efficiency as C1 is decreased, while the other set moves away from the highest efficiency under the same condition. The primary setting to watch, therefore, is that of C2.
Input = 50 Ohms; Output = 150 - j100 Ohms
Maximum permitted C1 = 172.6 pF
C1 172.5 C2 91080 L 1.37 delta 2.5
C1 150 C2 456 L 1.42 delta 3.0
C1 130 C2 223 L 1.52 delta 3.6
With respect to efficiency, the C-L-C Tee is less effective with capacitively reactive loads than with inductively reactive loads. With some load conditions, here a capacitive reactance of 100 Ohms combined with our standard 150-Ohm resistive component, a very low delta will not be possible with normal components. The best we can do is to keep delta as low as possible by following the common advice for C-L-C Tee tuners:
C-L-C Tees: Use the maximum capacitance possible, especially for C2, for a given matching situation.
However, even with a delta of 3.6 to 4, efficiency with a coil Q of 100 will be in the neighborhood of 96%.
SPC: The SPC (series-parallel capacitance) network is the more general case of which the C-L-C Tee is a specific instance. Note that the C-L-C results from the SPC if we lower the value of the capacitor in parallel with L to zero.
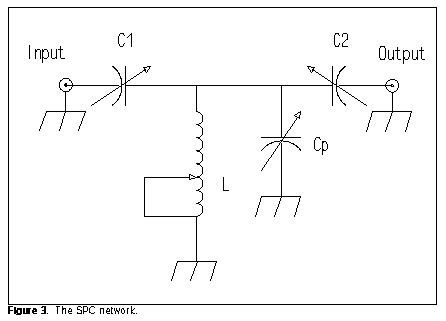
Ordinarily, the parallel capacitor is ganged as a dual unit with either C1 or C2. The requirement for a high-voltage dual-section capacitor has limited commercial production of SPC tuners. Figure 3 shows the more common configuration, with Cp and C2 ganged as equal-value units.
The SPC departs from the C-L-C Tee in two significant operational characteristics. First, the actual values required for a given impedance transformation will differ. Second, the SPC tends to tune much more sharply. I recommend the use of verniers on the capacitors for ease of tuning. However, the equation for determining delta for the SPC is the same as that given for the C-L-C Tee.
Input = 50 Ohms; Output = 150 +/- j0 Ohms
Maximum permitted C1 = 222.9 pF
C1 222.8 C2 6027 L 0.04 delta 58.8
C1 210 C2 362 L 0.64 delta 4.7
C1 180 C2 176 L 0.69 delta 4.6
C1 170 C2 152 L 0.75 delta 4.7
Input = 50 Ohms; Output = 150 + j100 Ohms
Maximum permitted C1 = 222.9 pF
C1 222.8 C2 154 L 0.82 delta 2.9
C1 220 C2 137 L 0.85 delta 2.8
C1 215 C2 118 L 0.87 delta 2.9
Input = 50 Ohms; Output = 150 - j100 Ohms
Maximum permitted C1 = 172.6 pF
C1 172.5 C2 91080 L <0.01 delta 1256
C1 140 C2 305 l 0.52 delta 9.1
C1 120 C2 172 l 0.76 delta 8.2
C1 110 C2 136 l 0.88 delta 8.3
The SPC tuner improves the harmonic rejection characteristics of the C-L-C Tee (which is inherently a high-pass filter), but apparently at the cost of lower efficiency. All three tables show the values surrounding the lowest value for delta obtainable under the given load conditions. The SPC appears to do better with inductive loads than with purely resistive transformations or capacitive loads. The value of delta increases for resistive and inductive loads as the ratio of output-to-input impedance increases, but shows a slight decrease for capacitive loads at higher ratios. Because tuning points are quite specific, no general rule of thumb is possible for the SPC.
The C-L-C PI, the C-L-C Tee, and the SPC are perhaps the most common networks in use at amateur stations these days. Of these, the C-L-C is the most common because it is the cheapest to produce commercially. PIs are less common at QRO levels because at least one of the capacitors must ordinarily have very high values of capacitance, which makes the component expensive.
At QRP levels, receiving capacitors from older BC receivers have more than enough power-handling capability to make any of these or other networks feasible for the station ATU. Indeed, the entire concept of using one ATU for all possible bands can give way at QRP levels to ATUs that are optimized for a small collection of bands. For example, large value capacitors needed for the lower HF bands often have minimum capacitance values that are too high for maximum ATU efficiency at the upper HF bands. For these bands, it is possible to use lower value capacitors having very low minimum capacitance values. Likewise, the smaller coils needed for these bands may avoid the so-called suckout effect by reducing the number of turns shorted out for a given band. Monoband QRP transceivers are common practice, especially with kits. It is feasible to optimize ATUs for each band and to include them in the same case (thus also eliminating connector losses as well). More next time.
Updated 1-31-99. © L. B. Cebik, W4RNL. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.