I have recently received a number of inquiries about calculating the length of wire needed to form the circumference of a single resonant square quad loop at numerous frequencies. Everybody seems to "know" that such a loop in the HF range requires use of the old formula
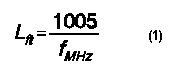
They also seem to know that this equation does not work at VHF.
In fact, this old formula, whose origin I mercifully do not know, does not work at HF either. It has been, is, and always will be wrong for common sizes of bare wire. I have heard by the unreliable grapevine that it is the formula to use at HF for insulated wire, where we have a shortening effect or velocity factor. However, being over 4% short, the formula exceeds the velocity factor effects of most wire insulations with which I am familiar.
#12 AWG bare copper wire requires a calculation constant of about 1043 at 28.5 MHz and a constant of about 1065 at 146 MHz. However, those numbers individually are good for one wire size at one frequency. There should be a more general solution that will get quad loop builders into the ballpark at any frequency and wire size. Therefore, let's look at the problem of figuring the wire for a single resonant quad loop all over again.
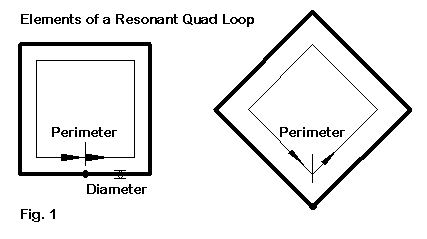
Fig. 1 shows us the basic ingredients for what we need. A single quad loop in free space has only two directly related dimensions: wire diameter and circumference length. If we express both measures in terms of wavelengths (or fractions of a wavelength), then the required perimeter length of the loop at resonance for lossless wire will be a direct function of the wire diameter. Remember that a fixed wire diameter, like #12 AWG wire (0.0808"), becomes a larger fraction of a wavelength as we increase the frequency. As we increase the wire diameter as a function of a wavelength, the loop circumference will also increase in terms of wavelengths.
The only reason we also need to know the frequency is so that we can translate the input wire diameter from a common unit of measure, such as inches or millimeters, into a fraction of a wavelength. If we uses feet and/or inches, then a wavelength, L, becomes
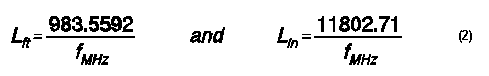
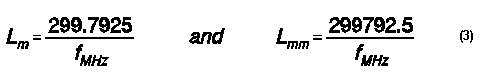
You can apply the length of a wave at your desired frequency to the wire diameter you select to get its diameter as a fraction of a wavelength.
For convenience in what follows, the following is a handy little table of the diameters of AWG wire sizes often used for building quad loops.
AWG Size Dia. Inches Dia. mm 18 .0403 1.0236 16 .0508 1.2903 14 .0641 1.6281 12 .0808 2.0523 10 .1019 2.5883
Once we have converted our wire diameter into a fraction of a wavelength, we can determine how long the perimeter of a single resonant quad loop must be in terms of a wavelength.
To find the relationship between the wire diameter and the perimeter length, I modeled a large number of quad loops and brought them to resonance, where resonance is defined as a feedpoint impedance with less than +/-0.1 Ohm of reactance. The process was considerably eased by using the model-by-equation facilities of NEC-Win Plus. Once I had placed variables for the wire dimensions and the wire diameter, a new model required only that I change two values on the equations page. Using this facility is how I came to realize that no matter what frequency I plugged into the model, the impedance did not change if I defined the variables in terms of a wavelength.
The restriction on this result is the use of lossless or perfect wire and a free space model. However, changing any model's material into copper or aluminum yields no significant adjustments to the result. The resistive component of the impedance grew to reflect the wire losses (an Ohm or two), and the remnant reactance near resonance remained less than +/-1 Ohm. Of course, ground effects will vary from application to application and must be the responsibility of the builder and user of the antenna. However, quad loops are relatively less sensitive to changes in height above ground than dipoles with free ends.
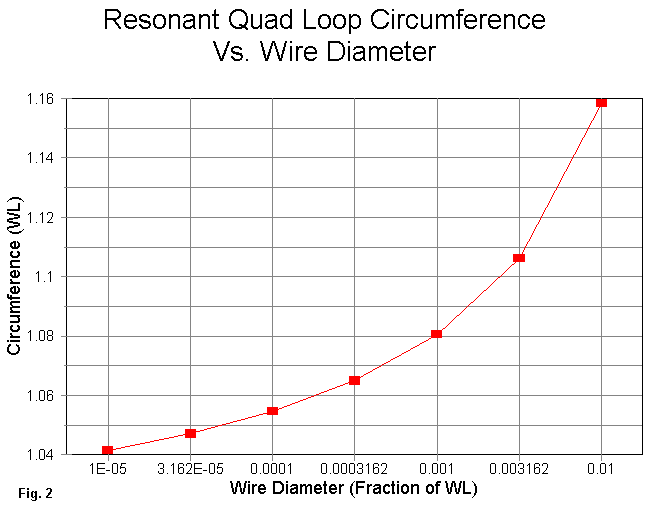
Fig. 2 shows the relationship between the wire diameter and the perimeter length, when both are expressed in terms of a wavelength. Note that the wire diameter axis is a log scale, and the "3162" steps are points at which the common log has a value of x.5. The graph is limited to wires sizes from 1.0E-05 to 1.0E-2, which covers the range of #18 on 80 meters to small tubing at VHF. As is evident, the relationship is not at all linear.
The following equation is a first order approximation of the curve in the graph.
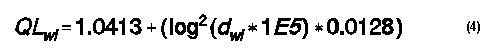
where QL is the perimeter length of the quad loop and d is the wire diameter, both in wavelengths.
The approximation is satisfactory for most amateur building projects, since the maximum error is about 2%, relative to the NEC models from which the algorithm was generated. The deviation from precise results can be shown in the following table which lists the reactance of quad loops modeled on the results of the algorithm.
Wire Size in WL Reactance of the Calculated Loop
.00001 - 1.1
.00003162 - 7.9
.0001 - 1.3
.0003162 +11.4
.001 +21.0
.003162 - 0.1
.01 - 1.7
The maximum error occurs at a wire size of about 0.001 wl. For larger and smaller wire sizes, the error in the algorithm is far less than 1%. Fig. 3 shows a combination of the modeled curve and the calculated curve as further means of tracing the relative deviations of the algorithm from modeled results.
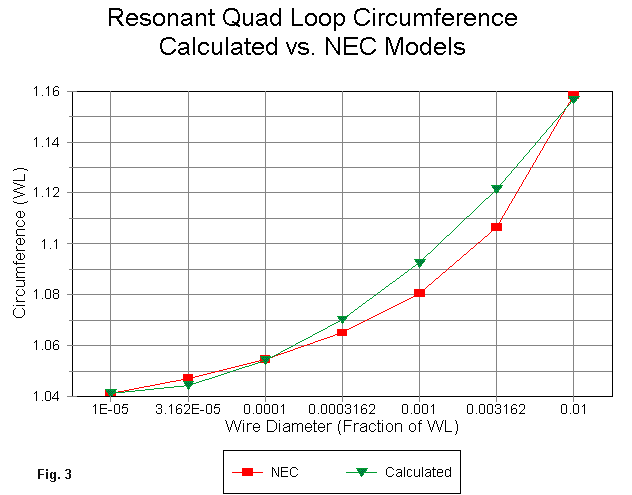
Translating the results in wavelengths into normal units of measure is simply a second exercise in applying the relationships in the earlier given equations. The required perimeter length can be transformed into any common unit for the frequency specified at the beginning of the exercise.
A Utility in GW Basic
To save you the trouble of doing the transformation and algorithm calculations for each possible quad you may wish to build, I have put the basics of the discussion above into a simple utility program. The listing of the GW Basic program follows.
10 PRINT "Program to calculate the perimeter length of a resonant quad loop." 20 PRINT "All equations correlated to NEC antenna modeling software." 30 PRINT "L. B. Cebik, W4RNL" 40 INPUT "Enter Desired Frequency in MHz:";F 50 PRINT "Select Units for Wide Diameter in 1. Inches or 2. Millimeters" 60 INPUT "Choose 1. or 2.";U 70 IF U>2 THEN 50 80 INPUT "Enter Wire Diameter in your Selected Units";WD 90 IF U=1 THEN WLI=11802.71/F:D=WD/WLI 100 IF U=2 THEN WLI=299792.5/F:D=WD/WLI 105 PRINT "Wire Diameter in Wavelengths:";D 110 L=.4343*LOG(D*10^5):LL=L^2:LM=LL*.0128:LN=LM+1.0413 120 PRINT "Perimeter Length in Wavelengths =";LN 130 WL=299.7925/F:PRINT "Wavelength in Meters =";WL 140 PM=LN*WL:PRINT "Perimeter Length in Meters =";PM 150 WF=983.5592/F:PRINT "Wavelength in Feet =";WF 160 PF=LN*WF:PRINT "Perimeter Length in Feet =";PF 170 END
The program let's you enter the wire diameter in either inches or millimeters. Anyone so inclined can add an AWG wire table module for direct entry of wire gauges. However, the table of diameters given earlier should satisfy most needs.
Line 110 does most of the calculating, with the algorithm broken into steps. You can modify the line to repackage the equation if you prefer that form. The program was written in GW Basic, which only recognizes log-base e (natural logs). But then, GW Basic was a product of the 1980s (my edition is dated 1987). Hence, the log functions contain a conversion factor for log-base 10 (common logs). You can expand the 0.4343 multiplier indefinitely for greater precision of calculation (say, to 0.4342945), but the common conversion factor is precise enough for virtually all applications. If you translate the program into another medium that recognizes both common (LOGx) and natural (LNx) logs, you should remove the conversion factor if you retain the "log" notation. Current spreadsheets--a common substitute for Basic--tend to have both functions.
Outputs (to screen only) include the input data, the wire size in terms of a wavelength, and the resulting perimeter length, also in terms of a wavelength. In addition, the outputs include the length of a wave in feet and in meters, along with the perimeter lengths in these units. I shall assume that conversion to inches or to mm or cm is a routine hand calculator job. However, you can feel free to doctor the utility program to include these outputs as well.
I tend to prefer working up utilities in GW Basic, since the listing makes all of the arithmetic transparent, both for error detection and for transferring the information to others. Indeed, if this item is downloaded as an ASCII file and the text trimmed away, most GW Basic programs will run the ASCII program listing.
Some Examples
Let's run a few examples through the calculating utility and see how they stack up to NEC models. First, we shall use #12 wire on 20, 10, 6, and 2 meters.
Frequency Wire Dia. Wire Dia Perimeter Perimeter
MHZ in. wl wl feet
14.1 0.0808 9.653E-5 1.0537 73.5026
Feedpoint Z Feedpoint Z
Perfect Wire Copper Wire
124.6 - j 1.5 126.3 + j 0.0
Frequency Wire Dia. Wire Dia Perimeter Perimeter
MHZ in. wl wl feet
28.5 0.0808 1.951E-4 1.0626 36.6716
Feedpoint Z Feedpoint Z
Perfect Wire Copper Wire
126.3 + j 5.9 127.6 + j 7.1
Frequency Wire Dia. Wire Dia Perimeter Perimeter
MHZ in. wl wl feet
51.0 0.0808 3.491E-4 1.0718 20.6697
Feedpoint Z Feedpoint Z
Perfect Wire Copper Wire
128.2 + j12.6 129.2 + j13.4
Frequency Wire Dia. Wire Dia Perimeter Perimeter
MHZ in. wl wl feet
146.0 0.0808 9.995E-4 1.0925 7.3598
Feedpoint Z Feedpoint Z
Perfect Wire Copper Wire
132.6 + j21.6 133.2 + j22.1
The series of #12 examples shows the "growth" in the wire diameter as a function of a wavelength. As well, the remnant reactance in the models that are based on the calculations reflects the curves shown in Fig. 3. Moreover, we can also see that as the loop circumferences grow, so too does the feedpoint impedance. However, as the wire diameter grows as a function of a wavelength, the losses reduce, as evidenced by the smaller differential between the resistive components of the perfect-wire and the copper wire impedances.
Before we leave you on your own, let's make a 146 MHz quad loop from 0.25" diameter copper and see what happens.
Frequency Wire Dia. Wire Dia Perimeter Perimeter
MHZ in. wl wl feet
146.0 0.25 3.093E-3 1.1207 7.5497
Feedpoint Z Feedpoint Z
Perfect Wire Copper Wire
138.0 + j20.6 138.2 + j20.8
As we pass over the point of maximum error we begin to see a reduction in the remnant reactance. But just how much deviation from true resonance does the 20 Ohms represent? The circumference of the calculated loop is 7' 6.6". A NEC model that brings the antenna to resonance within the specified limits of +/-0.1 Ohm reactance requires a circumference of 7' 5.4". The difference is just over 1% of the overall perimeter length. If we reference the VSWR of the calculated loop to 138 Ohms, the resulting value is 1.16:1.
To see the effects of ground on our calculated loop sizes, let's try the #12 28.5 MHz copper wire loop at various heights.
Height (wl) Feedpoint Z VSWR Relative
R +/- jOhms 127.6 Ohms
Free Space 127.6 + j 7.1 ----
0.5 125.3 - j 3.9 1.04
0.75 128.8 + j14.9 1.12
1.0 126.7 + j 1.2 1.01
1.25 128.3 + j11.7 1.10
The upshot of this table is that calculating the single quad loop via the algorithm will result in usable results for any common antenna height. Since the antenna impedance will slowly stabilize near its free space value as we further increase the height, VHF quad loops especially will show no adverse affects from the divergence between the model and calculation curves in Fig. 3.
The result is that the error level in the first order approximation--within the limits of the wire sizes chosen as the extremes--is not operationally significant. In fact, it is likely that construction methods will yield a greater variance from the NEC models than calculations via the algorithm.
Conclusion
It is certainly legitimate to ask why I have gone to such fussy levels of explanation and correlation with NEC models in the presentation of the simple BASIC program to calculate quad loop circumferences. The answer has two parts.
1. We began with a traditional wire cutting formula from sources unknown in the dim recesses of amateur radio's history. That formula has always simply been presented as if it were correct, and it has become embedded in the minds of antenna builders. I did not wish this presentation simply to present an alternative in equally simple terms, trusting only to the belief potential of readers.
2. The circumference of a single resonant quad loop turns out not to be amenable to a simple cutting formula at all. The required perimeter length is a direct consequence of the wire diameter selected for the loop. Although there are means--as shown in the Basic program--to calculate the required circumference from the wire size, getting used to the idea of how quad loops behave requires some degree of immersion. These notes have been designed to provide a small bath of quad loop calculation.
The program, of course, even within the limits of its accuracy, applies only to square and diamond loops that are individually resonant. Dimensions of the loops within a quad beam using 2 or more elements will differ, just as do the linear elements of a Yagi relative to a single resonant dipole.
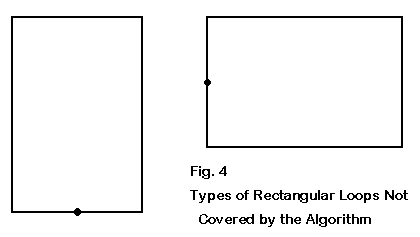
Moreover, the calculations will also require alteration for rectangular loops developed to achieve enhanced gain and a reduction of the feedpoint impedance to something closer to 50 Ohms. In general, the perimeter of such rectangular loops, when fed on the short horizontal elements shown in Fig. 4, will be somewhat longer than the circumference of a resonant square loop. Nevertheless, since squares are the most common form of loops, owing to the greater ease of construction, the little utility program in these notes should be serviceable for many antenna builders. An updated version of this program, using regression analysis results to derive more exacting dimensions, appear in the HAMCALC collection from VE3ERP.
Updated 03-01-2000, 03-23-2000. © L. B. Cebik, W4RNL. This item appeared in AntenneX, February, 2000. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.