
 The Monoband Log-Cell Yagi Revisited
The Monoband Log-Cell Yagi RevisitedMonoband log-cell Yagis have been designed using anywhere from 2 to 5 elements in the log cell itself. They may or may not use a reflector, and the number of directors has ranged from 1 to 3 in the designs I have encountered. Some log-cell designs have been very casual, while others (such as the Rhodes-Painter array1) have adhered to rigorous LPDA design procedures. Since the key to a log-cell Yagi is the log cell itself, it may be useful for us to spend some time exploring some facets of its design.
When the log cell has only 2 elements, one cannot distinguish it from a 2-element phased array. Indeed, one can build a successful beam by adding a director to a 2-element phased array--if the phased elements are properly designed. So let's begin with this simplified case and then proceed to more complex log cells.
Element phasing refers to the relative current magnitude and phase of each element in an array of elements. The current magnitude and phase are ordinarily read at the center of elements in symmetrical arrays in which each element length is in the vicinity of 1/2 wavelength.
By this accounting, a 2-element Yagi is a phased array, even though only the driven element is fed. The current magnitude and phase on the parasitic reflector is a function of coupled energy from the driver. We alter the current magnitude and phase on the rear element by varying the lengths of the elements and the spacing between them. For a simple 2-element driver-reflector Yagi, we have limited abilities to adjust the rear element relative current magnitude and phasing through modifying the antenna geometry itself. For example, the rear lobe gain of such arrays is rarely more than 12 dB below the main forward lobe.
By some judicious alterations of geometry, we can change the rear element current magnitude and phase to improve the depth of the rear null. One of the most remarkable designs in this regard is the Moxon rectangle. Folding the elements toward each other at the ends results in a rear element current magnitude and phase for the element spacing that yields a very deep rear null--often better than 35 dB below the main forward lobe at the design frequency.
As an alternative to the limitations of geometric means of altering the rear element relative current magnitude and phase, we can directly feed both elements of the array. Let's adopt the convention that the forward element will be set at a relative current value of 1.0 at a phase angle of zero degrees. With this constant, we may then focus on the current magnitude and phase angle of the rear element (always relative to the constant values of the forward element).
The required current magnitude and phase on the rear element will depend upon several variables. First are the lengths of the elements. We may make them equal or unequal. Moreover, we may set the lengths close to resonance or distant from resonance. Each variation will show changes in either or both the magnitude and the phase on the rear element for a desired operating characteristic of the array. For example, if the elements, whether equal in length or unequal, show a feedpoint impedance close to resonance when only the forward element is fed, then the phase angles of equal length and unequal length element sets will be very close in value, although the current magnitudes will vary for a given spacing and operating condition.
Second, element spacing will have a major affect on the required rear element current magnitude and phase for a desired operating characteristic. Third, the desired operating characteristic will also alter the current magnitude and phase for any set element lengths and spacing.

As a little experiment, let's look at what happens when we phase both elements of two different array pairs, shown in Fig. 1. At a spacing of about 0.125 wavelength, the unequal element pair makes up a very workable 2-element Yagi for 28.5 MHz, when only the forward element is fed. At the same spacing, the equal-length pair is close to resonant, but with a typical dipole pattern.
Now let's set as our operating goal achieving a maximum rear null 180-degrees from the peak of the forward lobe. We can define the null as adequate if it exceeds -50 dB relative to the forward lobe. This value would exist only over a tiny bandwidth, but for study purposes, it is a goal that modeling programs, such as NEC-4, can easily show. We shall vary the distance between the elements in 0.05 wl increments. For each distance, we shall change the current magnitude and phase on the rear element until the desired null is achieved.
Phasing 2 Elements for Maximum Rear Null
Equal vs. Unequal Element Lengths
Rear Element Current
Spacing Spacing Magnitude Phase Free-Space Front-to-Back
wl inches (relative) degrees Gain dBi Ratio dB
Designed for Maximum Rear Null:
Equal-Length Elements (196.8" x2 at 28.5 MHz)
0.05 20.7 1.035 163 6.55 >50
0.1 41.4 1.07 145 6.46 >50
0.15 62.1 1.09 125.5 6.18 >50
0.2 82.8 1.09 106 5.76 >50
0.25 103.5 1.07 87 5.14 >50
0.3 124.2 1.045 69 4.26 >50
0.35 144.9 1.02 51 2.72 >50
0.4 165.7 1.00 34 0.31 >50
Unequal-Length Elements (192" forward, 208.1" rear at 28.5 MHz)
0.05 20.7 0.925 163.3 6.57 >50
0.1 41.4 0.945 145 6.45 >50
0.15 62.1 0.955 126.0 6.19 >50
0.2 82.8 0.95 106.7 5.77 >50
0.25 103.5 0.94 88 5.16 >50
0.3 124.2 0.92 69.5 4.21 >50
0.35 144.9 0.90 51.8 2.73 >50
0.4 165.7 0.88 34.5 0.28 >50
Note 1: All forward element currents set at a relative magnitude of 1.0 at 0ø phase angle.
Note 2: All values of rear current relative magnitude and phase angle taken when the rear
null passed -50 dB relative to the forward lobe.
Note 3: Elements are 1" diameter aluminum.
Table 1: Phasing 2 elements for maximum rear null using equal and unequal element
lengths.
Table 1 shows the results for both element pairs. As predicted, the current phase for each step is virtually the same for both arrays, but the required current magnitude on the rear element is different according to whether the elements have the same or different lengths. Other element lengths we might have chosen would have resulted in other values.
For each increase in spacing, the current magnitude changes very little with each array, but the required phase angle on the rear element shows a continuous decrease. In short, there is no single ideal spacing for achieving a deep rear null. Instead, for any spacing, there is a current magnitude and phase angle that will achieve the null.
Phasing 2 Elements for Maximum Forward Gain
Equal vs. Unequal Element Lengths
Rear Element Current
Spacing Spacing Magnitude Phase Free-Space Front-to-Back
wl inches (relative) degrees Gain dBi Ratio dB
Designed for Maximum Rear Null:
Equal-Length Elements (196.8" x2 at 28.5 MHz)
0.05 20.7 1.02 173 7.32 7.64
0.1 41.4 1.03 165 7.35 7.19
0.15 62.1 1.02 158 7.23 6.90
0.2 82.8 1.03 152 7.03 6.00
0.25 103.5 1.03 147 6.76 5.03
Unequal-Length Elements (192" forward, 208.1" rear at 28.5 MHz)
0.05 20.7 0.91 173 7.33 7.70
0.1 41.4 0.92 166 7.36 7.22
0.15 62.1 0.92 159 7.24 7.03
0.2 82.8 0.92 150 7.04 6.59
0.25 103.5 0.93 147 6.77 5.13
Note 1: All forward element currents set at a relative magnitude of 1.0 at 0ø phase angle.
Note 2: All values of rear current relative magnitude and phase angle taken when the
forward lobe reached a peak gain, beyond which gain fell off.
Note 3: Elements are 1" diameter aluminum.
Table 2: Phasing 2 elements for maximum forward gain using equal and unequal element
lengths.
Much of antenna element phasing theory is devoted to the achievement of rearward nulls. Little attention has been given to achieving maximum gain from the array. Let's look at Table 2 to see what the effects of changing space might have on the required rear element relative current magnitude and phase for this goal. For spacing from 0.05 through 0.25 wavelengths, the required current magnitude for each array remains relatively constant. However, the required phase angle decreases with increased spacing, but at far less than the rate for achieving a maximum rearward null. Maximum gain does not occur with the closest spacing, but in the vicinity of 0.1 wl. As one might expect, the front-to-back ratio of two elements becomes mediocre (at best) when the goal is maximum gain.
The reason I have presented the table of values for maximum forward gain is simple: when designing an array with a pair of phased elements plus some further element--such as a director--the proper design procedure is to set the phased pair of elements for maximum forward gain. It will be the added element (or elements) that shapes the antenna's operating pattern to the desired specifications.

Let's examine a test array consisting of a phased pair plus a director, as shown in Fig. 2. The phased portion of the array consists of unequal-length elements. In this design, a 50-Ohm phase line about 69.3" (for 0.66 VF line) provides the requisite current magnitude and phase transformation. (Although 50-Ohm parallel line is not possible using round conductors, parallel strips can be used, with the velocity factor adjusted back to 1.0. If the boom is RF transparent, then coaxial cable can also be used.) The design frequency for this test array is 28.5 MHz.

Fig. 3 shows two things at once. One azimuth pattern show what happens if we omit the director. The phased pair is set for maximum gain--or very close to it. Adding the director increases gain, but even more significantly, the director increases the front-to-back ratio to a very respectable level. (Even in pure Yagi design, reflectors do not control the front-to-back ratio nearly so much as do the directors.)

Let's look more closely at the performance of this antenna across the first MHz of 10 meters. Fig. 4 graphs the gain across the band, with the 4-element Yagi presented as a comparator in Part 1 as a standard for comparison. Both antennas are about the same overall length--a bit over 12.5' long. The 3-element array (labeled "3-L 2-cell" on the graphs) shows a very steep gain curve, especially when compared to the stable 4-element Yagi curve. At the design center frequency (28.5 MHz), the 3-element array actually show slightly better gain.

The front-to-back curves appear in Fig. 5. The 3-element array shows a very high peak value at the design frequency, but exceeds 20 dB for less than half of the bandwidth in the graph. The stability of the 4-element Yagi front-to-back ratio across the band is self- evident.

The native feedpoint impedance of the 3-element array is about 15 + j23 Ohms. This value is amenable to a beta match using an open stub (instead of the usual shorted stub used when the reactance is capacitive). 2:1 SWR operation across all of the first MHz of 10 meters is not possible, as shown in Fig. 6.
The narrow-band characteristics of this array illustrate in part what happens when 2- element phased pairs are operated too close to maximum gain. Nevertheless, scaled for any of the WARC band, this array might provide quite good performance with a minimum of elements.
Larger log cells are often designed exactly as one might design a full LPDA, except that the design will be for a single band and also be considerably shorter that an independent LPDA, as illustrated in Fig. 7. The design principles for LPDAs are fully described in The ARRL Antenna Book and in standard professional antenna compendia, so I shall not review them in detail here.2 Most of the math can be passed through a computer design program, such as LPCAD by Roger Cox, WB0DGF.3 To these resources, we can add only a few practical notes.

First, many LPDA and log-cell designers select too high a phase-line impedance to achieve maximum gain from the array. My experiences designing a monoband LPDA suggest strongly that the lowest practical phase-line impedance yields the highest gain and overall operating characteristics. This procedure may require careful rethinking of the mechanical aspects of the design, especially implementing a low impedance phase line with double-boom construction or other means.
Second, the fatter the elements, the higher the cell gain and the wider the bandwidth for the desired operating characteristics. For monoband cells and LPDAs at 10 meters, elements should be at least 0.5" in diameter, with diameters up to 1" desirable.
Third, the closer one attends to making the cell in accord with the LPDA principles in which both element lengths and spacings decrease together, the wider-band the resulting cell and array. One test of a good log cell--as we shall illustrate in more detail in Part 3--is that the feedpoint impedance of the log cell without added parasitic elements should not radically change from the feedpoint impedance with those elements in place.
Even with these practical notes in mind, a good modeling program is a major aid to log-cell Yagi and LPDA design. Every cell design requires Tw2 (Twisting and Tweaking), that is, final adjustment of element lengths and spacings, along with phase-line impedance value settings, to produce the desired operating characteristics of the antenna.
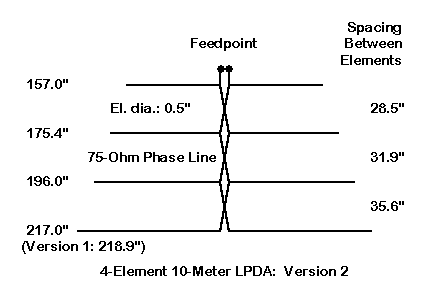
To illustrate this point, let's look briefly at an LPDA--a log cell without additional parasitic elements--for 10 meters. Fig. 8 shows the outlines of the antenna, which is given in two versions, one with a 217" rear element, the other with a longer 218.9" element. The 75- Ohm phase line can be achieved with twin square booms or with facing aluminum strips. Although the basic dimensions emerged from LPDA calculations, the final dimensions are the result of considerable tweaking.
Because this antenna sought to combine smooth curves of both acceptable gain and an adequate adequate front-to-back ratio, a ratio of about 0.90 was selected. That is, each element forward of the one to its rear is about 0.90 of its length. Moreover, the element spacing moving forward is also 0.90 of the spacing between the next elements rearward. As we shall see in Part 3, practical log cell design for log-cell Yagis employs a ratio closer to about 0.95.

The gain across the entire span of 10-meters appears in Fig. 9, with the curve for the 4-element wide-band Yagi from Part 1 added for comparison. The LPDAs and the wide-band 4-element Yagi are both 8' long. Version 2 of the LPDA provides slightly higher gain than version 1. Both curves are more stable across the band than is the Yagi curve.

Although version 1 of the LPDA has slightly less gain than version 2, the first version shows an overall better front-to-back profile across the band, with a very high peak at 28.5 MHz, as shown in Fig. 10. Both version of the LPDA exceed the Yagi in average front-to- back ratio across the band.

In Fig. 11, we have the 50-Ohm SWR curves for all three antennas, none of which requires a matching network. With a peak SWR value of 1.35:1, there is little to choose among the antennas in this department.
A 4-element log-cell designed for 10-meters without parasitic elements is capable of better than 7 dBi free-space gain all across the band with excellent front-to-back ratio values and an easy direct coax match--all on an 8' boom. This becomes another standard of comparison for log-cell designs by giving us a new question for our list: what advantages do parasitic elements give us?
A partial answer to that question showed up in the narrow-band, high-gain, high-front- to-back design we discussed earlier. We can add some gain and possibly improve the front- to-back ratio. We shall do that by designing our log cells to enhance gain rather than striving for a balance of operating characteristics. Parasitic elements will finish the job of tailoring the pattern.
We shall encounter some practical designs that casually design the cell and some that design it very carefully. The results of each practice will show themselves in the resulting antenna performance. But all of that is for Part 3.
1. P. D. Rhodes, K4EWG, and J. R. Painter, W4BBP, "The Log-Yagi Array," QST, Dec, 1976. The main elements of this article are reprinted in The ARRL Antenna Book, 18th Ed., pp. 10-25 to 10-27.
2. See The ARRL Antenna Book, 18th Ed., pp. 10-1 to 10-6, plus such professional references as Johnson and Jasik.
3. LPCAD has been available at many world wide web archives, but availability may vary in this fast-changing medium. LPCAD 2.8 should appear in 2000.
Updated 3-5-2000. © L. B. Cebik, W4RNL. A version of this item appeared
in The National Contest Journal, Mar-Apr, 2000, 10-13. Data may be used for
personal purposes, but may not be reproduced for publication in print or
any other medium without permission of the author.