So let's take a patient look at convergence testing. Our aim will be not just to be able to do it, but as well to understand why we should always do it.
Both NEC and MININEC calculate antenna properties based on the division of the antenna elements into a collection of short wires. Within the program limits, the shorter, the better. However, both NEC and MININEC make use of complex calculation matrices that take time to fill and resolve. The more segments we have, the longer the run time.
Because we are impatient, a bad habit has set in among many program users: to divide the antenna elements into as few segments as possible, again within certain generalizations in the instruction manuals. For MININEC, the recommended minimum number of segments per half-wavelength is 10, while for NEC-2 it is 9 or 11. (When center feeding an antenna element, use an even number of segments for MININEC and an odd number of segments for NEC.)
What we often forget is that neither program is absolutely stable, and the best we can hope for is relative stability. What stability refers to is the fact that if we change the number of segments per half-wavelength, without changing the overall dimensions, the program will produce different output data. What we strive for is a number of segments per half wavelength that--as we change the segmentation--produces output data differentials that are too small to be operationally significant. Of course, what counts as being operationally significant depends on the modeling goals for a given project.
We can illustrate the instability of the program by making some runs with an ordinary 20-meter dipole, as shown in Figure 1. (In all figures, the heavy black "dot" represents the source or feedpoint. It is shown as a dot rather than as a break in the wire to indicate that the wire is continuous and the source is inserted in series with the wire.) The only factor we shall change from model run to model run is the number of segments into which we divide this half-wavelength of wire.

For NEC-2, we can make a table of the results:
Segments Gain in dBi Source Impedance (R+/-jX) 11 7.97 67.51 - j0.22 15 7.98 67.50 + j0.34 21 7.98 67.52 + j0.24 25 7.99 67.53 + j0.32 31 7.99 67.54 + j0.42 35 7.99 67.55 + j0.46 41 7.99 67.56 + j0.53 45 7.99 67.56 + j0.56
This example is the source of the fatal temptation to always use the minimum number of segments. It is operationally stable at the lowest level of segmentation for any purpose I can think of, since I have no instruments capable of trimming an antenna to the variations shown in the numbers.
However, the table does illustrate that the numbers in fact do change with the level of segmentation. As the first 4 lines of the source impedance entries show, the numbers may drift in either direction until some large number of segments are used.
A similar situation exists with MININEC. The segmentation varies from the NEC table to accommodate the source location.
Segments Gain in dBi Source Impedance (R+/-jX) 10 7.83 67.51 - j6.78 16 7.85 68.19 - j7.71 20 7.85 68.40 - j7.57 26 7.86 68.59 - j7.22 30 7.86 68.67 - j7.01 36 7.86 68.76 - j6.70 40 7.86 68.81 - j6.50 46 7.86 68.87 - j6.26
The intrinsically higher level of reactance is a function of MININEC's growing error in resonant length as the frequency climbs. Some programs correct for this error; others do not.
Nevertheless, we find a similar drift in values with increasing segmentation. However, for operational purposes, the numbers give us confidence that a dipole constructed from these dimensions would work perfectly well with only such trimming as our yard clutter and local terrain might make necessary.
One common way in which we often fail to observe even the minimum recommended segmentation is when we increase the frequency of operation of an antenna without altering the number of segments. Figure 2 shows the same antenna, but now operated at 28.0 MHz.

The results for NEC-2 are the following:
Total Segments Gain in dBi Source Impedance (R+/-jX) 11 9.58 3813 + j1438 23 9.61 4306 - j 376 33 9.62 4120 - j 945 45 9.62 3928 - j1266 55 9.62 3810 - j1415 67 9.62 3705 - j1529
Although the gain stabilizes as soon as we use at least 11 segments per half-wavelength, the source impedance continues to move around considerably. since we would likely feed this antenna via a parallel transmission line and antenna tuner, we might easily overlook the variance.
However, the antenna as presently used can be viewed as two end-fed half- wavelength dipoles physically coupled. End feeding near resonance yields large changes in source impedance with very small changes in physical dimensions. Hence, changes in segmentation yield possibly significant differences in source impedance.
MININEC shows a similar set of figures:
Total Segments Gain in dBi Source Impedance (R+/-jX) 10 9.55 3401 - j1646 22 9.56 3537 - j1519 32 9.56 3485 - j1568 44 9.56 3431 - j1616 54 9.56 3399 - j1643 66 9.56 3366 - j1669
Interestingly, the source impedance figures for MININEC appear to be more stable than those for NEC-2. It should be remembered that all MININEC source impedance figures are calculated based on perfect ground, whatever the ground used to determine the far field figures. (Medium earth is used throughout these examples.) NEC-2 calculates source impedance based on the Sommerfeld-Norton ground conditions specified for the antenna.
In determining whether a satisfactory level of convergence has been achieved, the program user must determine how much variance is necessary to make it significant. The following driver-director 10-meter Yagi, shown in Figure 3 at a height of 1/2 wavelength, might be instructive here.

NEC-2 tabulates the results as follows:
Segments/Element Gain in dBi Front-to-Back in dB Source Impedance (R+/-jX) 11 10.84 14.11 21.11 - j23.57 15 10.88 14.34 20.66 - j22.64 21 10.91 14.55 20.30 - j21.87 25 10.92 14.64 20.15 - j21.54 31 10.93 14.73 19.99 - j21.19 35 10.94 14.78 19.91 - j21.01 41 10.94 14.84 19.81 - j20.78 45 10.95 14.87 19.75 - j20.66
It might appear that, although the gain and the source impedance are fairly stable, especially in models using at least 21 segments per element, the front-to-back ratio continues to change at higher rate. However, from an operational standpoint, changes of a dB in this ratio are not especially detectable, and hence, the model might well be said to converge at about 21 segments per element--or less, if the needs are less critical.
Moreover, since we would likely use a matching system, such as the beta match or a series feedline section, between the feedpoint and the main 50- ohm coaxial feedline, the variations in the source impedance are unlikely to fall beyond normal adjustment limits. Hence, the home constructor might well judge the model to be well converged at the lowest level of segmentation. In terms of comparative design analysis, we might hold out for segmentation of at least 20 segments per element.
The corresponding MININEC model was run at the same frequency. Hence, its performance figures will be less impressive, since they reach a peak at a different frequency. However, for our purposes, the table shows a similar level of stability as the NEC-2 table above.
Segments/Element Gain in dBi Front-to-Back in dB Source Impedance (R+/-jX) 10 10.49 10.71 21.91 - j29.20 14 10.53 10.90 21.72 - j28.79 20 10.56 11.18 21.29 - j27.75 24 10.61 11.34 21.01 - j27.11 30 10.64 11.47 20.81 - j26.40 34 10.65 11.57 20.63 - j25.79 40 10.68 11.71 20.37 - j25.27 44 10.68 11.75 20.31 - j24.94
Although stable enough for most purposes at the lowest level of segmentation, the figures are highly stable once we use more than 20 segments per elements.
Symmetrical structures, even of some complexity tend to show a higher level of stability than non-symmetrical structures, even of similar types. To illustrate the point, let's compare a pair of triangular designs, vertically oriented. The first is a right-angle delta for 7.15 MHz, shown in Figure 4.

Despite its angularity, the antenna is quite stable once the segments are shorter than the maximum recommended length. The segmentation column shows the number of segments in each angular leg, and then the horizontal leg.
Segments Gain in dBi Source Impedance (R+/-jX) 6/6/8 1.73 63.83 + j1.49 12/12/17 1.90 60.95 - j0.29 18/18/25 1.89 60.99 - j0.77 24/24/34 1.89 61.03 - j1.03 30/30/42 1.89 61.06 - j1.18
The lowest level of segmentation results in segments longer than the maximum recommended length. Beyond that level, the model shows excellent stability over many levels of segmentation, despite the fact that the source is moving slightly each time, since it is specified as a percentage of the left leg.
One might be tempted to also model this antenna via MININEC. However, to do so would be to violate the limits of reliability with respect to the height of the antenna above ground. In general, as an antenna is brought closer to ground than about 0.2 wavelength, the gain increases inaccurately. For example, a fully length-tapered version of this antenna shows a MININEC source impedance of 64.5 - j23.6 ohms, somewhat off the NEC-2 mark, but not drastically. However, the antenna also shows a wholly unrealistic gain of 3.63 dBi.
For comparison, let's look at model of another triangle, one developed by W6RCA and shown in Figure 5.
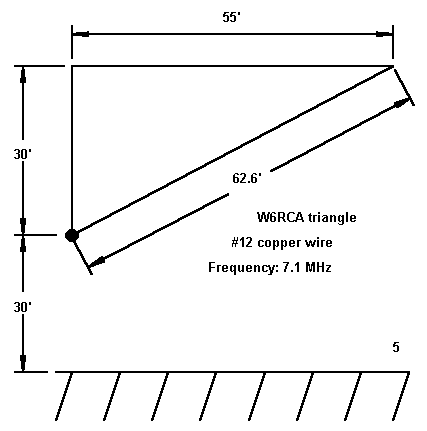
Relative to the plane of the antenna facing us, the antenna is not symmetrical on either side of a line one might draw at to bisect the source. Although the angularity of the antenna might lead us to believe that its model will behave similarly to the right-angle delta, the NEC-2 table tells a different story when using a split-current source feed. (This feature is available on programs such as EZNEC. The model shows much less instability when using a split-voltage feed.) The segmentation column refers to the number of segments in the vertical leg, the horizontal leg, and the diagonal leg, respectively.
Segments Gain in dBi Source Impedance (R+/-jX) 4/8/9 4.33 62.05 - j10.08 7/12/14 2.87 47.99 - j 5.77 9/16/19 2.45 44.10 - j 2.08 11/21/23 2.32 42.65 - j 0.26 13/25/28 2.24 41.83 + j 1.95 16/29/33 2.21 41.37 + j 3.73 18/33/37 2.19 41.19 + j 4.53
As with the right-angle delta model, the initial segmentation yields segment lengths longer than the maximum recommended values, and this fact is reflected in the unrealistically high gain and source impedance. By the point of maximum segmentation in the exercise, the model has stabilized to an operationally useful point--sufficiently so that the dimensions promise to make a good starting point for building such an antenna. However, the rate of change from one level of segmentation to the next is still significantly higher than it is for symmetrical antennas such as the dipoles, the Yagi, or the right-angle delta.
Inadequate segmentation on the split current-fed model does not just affect the gain and source impedance numbers. In fact, the entire far field pattern changes when comparing minimal segmentation models with adequately segmented models. Figure 6 compares the elevation pattern perpendicular to the face of the triangle for the 21-segment model and the same pattern produced by the 88-segment model. The latter is typical of the patterns of the group of more nearly converged models. The difference is not merely a matter of gain, but as well the correct portrayal of higher-angle radiation from the antenna. (Again, the model does not show the dramatic change in pattern shape when split-voltage-fed.)

Unlike the right-angle delta, the W6RCA triangle can be modeled via MININEC, since the bottom is about 0.22 wavelengths above ground. Even though MININEC advises against modeling with small numbers of segments when an antenna geometry contains right or acute angles, the exercise may be instructive. Again, for this example, the model is split-current fed.
Segments Gain in dBi Source Impedance (R+/-jX) 4/8/9 3.43 64.17 - j210.2 7/12/14 3.28 50.00 - j125.6 9/16/19 3.32 45.72 - j 89.5 11/21/23 3.37 42.66 - j 68.4 13/25/28 3.38 42.02 - j 54.2 16/29/33 3.39 41.68 - j 43.3 18/33/37 3.39 41.68 - j 36.8
Although the model comes to show reasonable stability, its reported gain is well above that of the NEC-2 model, largely because it is near the border of reliability. This fact is significant, since many MININEC users think of the 0.2 wavelength height limit as a kind of breaking point. It is not.
Instead, it is a region where gain reports on different types of antennas become unreliable at different actual heights above ground.
The large swing of reactance in the source impedance is due to the fact that MININEC models in effect cut off sharp interior corners. The longer the length of individual segments meeting at an acute angle, the more wire is effectively trimmed in the computation of impedance and current interactions. As the segments grow shorter, the antenna gradually approaches its physical full size. A fully length-tapered version of the antenna model showed a gain of 3.38 dBi (still unreliably high), and a source impedance of 40.32 + j5.20 ohms, not far off the NEC-2 model.
The lessons taught by the W6RCA triangle are numerous and useful. First, it is unsafe in terms of model reliability to use the minimum number of segments per half-wavelength recommended for wires in the model by the program. These program recommendations are based upon linear elements and apply at most to symmetrical antenna geometries.
Second, it is also unsafe to assume that some arbitrary larger number of segments per half-wavelength will automatically yield a reliable model. The W6RCA triangle remained less stable with 44 segments per half- wavelength than many of the other models with under half that number.
The designer must make a series of convergence tests and reach a decision concerning the adequacy of stability in the model based on standards brought to the modeling exercise from a knowledge of the goals of the overall project. In some cases, stability adequate to one task may not suffice for another.
Third, inadequate convergence holds the potential for producing a model that misrepresents antenna performance in every way: gain, front-to-back ratio (if applicable), source impedance, and field pattern shape and strength. Although convergence alone cannot guarantee the adequacy of a model, it is one necessary condition to that goal.
Antenna modeling can be a very significant short-cut in the design and building of antennas. However, we can achieve the savings only if we do not take short-cuts with the modeling process itself. Convergence testing is one of those steps we should never omit, lest the minutes we save at the computer testing our models end up costing us hours of frustrating time spent trying to adjust an antenna that is based upon an inadequate model.